一种归一化的信息系统安全分计算方法
0 摘要
本文设计了一种以百分制方式定量评估系统安全性的方法,通过风险赋值和此基础之上的计算,得到一个符合系统整体安全水平的分数。该方法应满足适用于不同资产规模的系统,通过调节系统参数,可以对不同系统的安全水平进行横向对比。该方法对低危风险不敏感,更关注高危风险,也就是说脆弱性的利用的难易程度和实际危害最终将在整体分数上体现。同时,当一个系统被多个高危漏洞影响的时候,系统的安全水位不会因高危漏洞的数量变多而线性降低,它只会无限趋近于某一个极限值。
1 引言
对于一个存在风险的信息系统,通常通过量化指标的方式对其进行安全性评估。这里的安全性评估代表被攻击后能被成功入侵的可能性数字表示(这个数字的数值代表被成功入侵的难以程度,但不直接表示概率)。在很多SIEM或SOC系统中,可以看到的一种做法是给每一个风险点进行分数赋值,找出所有的风险并累加分数就可以得到一个风险分数。有些系统会根据风险点的某些属性设置权重,最后通过加权计算得到风险分数,这些方法本质上都是把分数进行累加。这种方法很简单,但是存在一个明显的缺陷就是当一个信息系统规模特别庞大时,如果出现的低风险漏洞很多,也容易累加出一个很高的分数。但熟悉渗透测试的人都知道,许多低风险漏洞在实际对抗中没有任何价值。因此这样计算出的分数对于描述系统的实际风险具有较大的误差。从经验上讲,我们希望对信息系统安全状态的描述更倾向于给出一个符合直觉的判断,举例来说,如果以百分制作为标准,当一个系统的安全分是90分的时候,我们感觉这个系统总体上是安全的,但是当它的安全分是10分的时候,我们认为它可能存在比较大的安全隐患。(当然我们也可以对调安全性和风险性的坐标,用“风险分”代替“安全分”,相应的描述也应该是相反的。)
基于这样的背景,就需要一个客观的算法对系统的安全水平进行评估。它需要对风险因素的数量规模不能那么敏感,同时又要反应系统被攻击后失陷的难易水平。对于具体的设计原则,后文中有更详细的介绍。
需要指出的是,这种方法不同于标准的风险评估中通过“资产”“威胁”“脆弱性”三要素进行的风险评估方法,仅仅作为一种符合日常需求的“最佳实践”方案。
2 方案设计
2.1 需求
如在引言中提到的,系统安全性的评估有时候需要一个符合直觉感受的定量测算的方法。这种方法可以在不同的系统上测算,得到的分数可以用于不同系统间横向比较,而分数的高低可以反应系统安全水平的差异,而这种差异也是可以被验证的。也就是说,当A系统的风险分高于B系统时,就可以通过渗透测试验证A系统比B系统更容易被攻陷。而对于资产和漏洞差别较大的系统,需要有一个统一的参考系才能建立这把统一的标尺。通常习惯于使用百分制作为这个参考系,0和100是这个参考系的两极。
在明确了度量方法的形式以后,它的第二个重要领域则是如何将系统本身的风险因素反应在分数上。一个系统内部和外部通常具有不止一个风险因素,不同的风险因素带来的影响和危害程度不尽相同。在信息安全领域,最严重的风险通常包括系统权限被完全控制、系统宕机拒绝服务、敏感数据泄露等等,如果某个系统具有一个这样严重的风险因素,那么他的安全分就应该大打折扣,而具备多个风险点的时候,累加扣除的风险分值反而是趋于收敛的。因为系统安全分的下限不会变成负数,而从经验上看,一个系统被击穿一次和击穿数次,都证明它的安全性很差,对于一个在要害部位被捅了刀子的人而言,一刀和几刀没有太大差别,最终结果是一样的。
基于以上考虑,我们把度量方法的需求提炼归纳为以下几条:
- 满分为100分,取安全性作为分数的正方向,及风险水平与安全评分负相关,评分越高,安全水位越高。
- 系统对不同严重程度的风险因素敏感程度不同,越严重的风险影响越大,越轻微的风险影响越小。
- 在不同的评分区间对漏洞的严重等级敏感程度不同,当漏洞较少时,单个漏洞造成的扣分较多,漏洞较多时单个漏洞扣分较少。
- 越严重的风险对分值的影响越大,而且严重程度的影响会随着风险赋值几何增加,而不是线性增加。例如风险因素分为1、2、3、4四个档位,它们最终造成的扣分可能是1、5、20、50。
- 评分的下限是0分,不会出现负分的情况。
2.2 分析
有了整体的方向,就开始构思如何去实现。
首先困扰我的,是如何把风险累加的结果设计成有限的,这个过程不应该人为的控制,而是由于算法的数学特性自动反应在结果上的。于是我想到了有限函数,函数在无穷远处逼近一个极限,这样才能保证当风险因素不断叠加后,分数不会低于0。而风险因素的变化对分数的影响是一致的,于是我想到函数的单调性,于是这个函数应该是一个单调有限函数。回忆学过函数类型,一元一次函数、一元n次函数都没有极限,三角函数不单调,剩下的就是指数函数、幂函数和双曲线函数。
其次,当风险因素的赋值是线性的,而不同的赋值对分数的影响是非线性的。我想到给输入的风险因素赋值加一个权重系数,用于放大不同等级的风险对分数的影响。改变权重系数,可以调节对不同等级风险的差异放大的效果。
第三,函数应该是单调递减的,没有风险的时候分数是100,随着风险的增加,安全分不断降低(安全分=100-风险分),直至趋近于0。因此在定义域是0到正无穷的范围内,计算风险分的函数的变化区间是0到某个数值,最终通过乘一个系数调整成0到100。
综合以上要求,我们发现幂函数可以通过一些变换来达到想要的效果,因此我们把目光锁定在e的x次方这个表达式上。
2.3 设计
- 原始表达式
首先,风险转换成分数通过累加得到总的风险值,而我们希望安全分定义在从0到100的区间,因此我们让安全分等于100减去风险分,这样当没有风险的时候,安全分等于100,当风险趋于无穷大的时候,安全分趋近于零。将指数函数f(x)=EXP(x)先做关于y轴的对称变换,再做关于x轴的对称变换,得到函数f(x)=-EXP(-x),函数的值域为[-1,0),并且函数单调递增。我们希望函数的值域在0到正100之间,那么我们将函数向上平移1个单位,然后给函数乘以系数100,就可以得到当定于域为[0,+∞)时,值域为[0,100)的单调递增函数,即f(x)=100[1-EXP(-x)]=100-100·EXP(-x)。
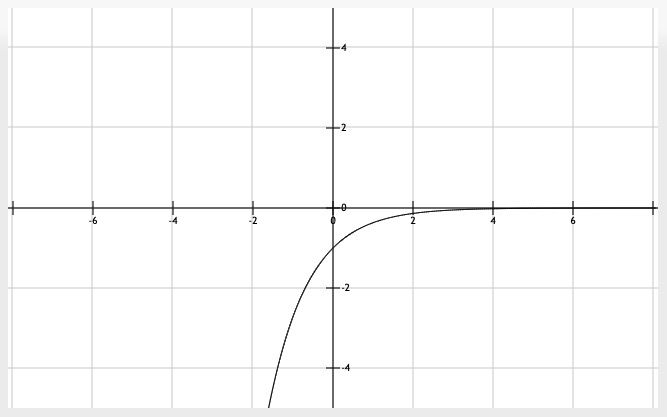
图1 f(x)=-EXP(-x)图像
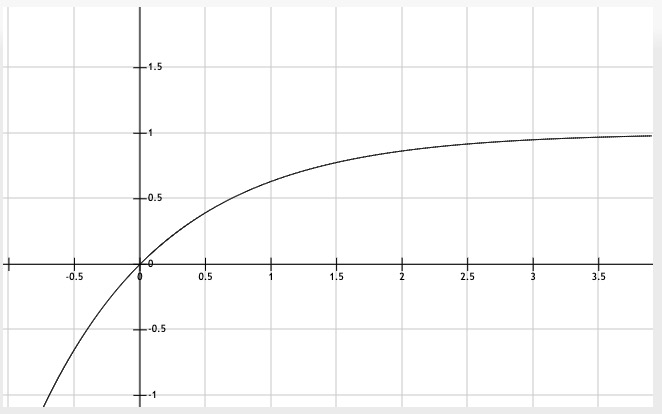
图2 f(x)=1-1·EXP(-x)图像
我们希望风险分数和赋值是正相关的,同时希望风险分数和风险的数量是正相关的,那么自变量x是关于全部风险因素的函数,即g(z)=k1·z1+k2·z2+……kn·zn。其中,zi代表每个风险因素的风险赋值,ki代表权重系数,由于f(x)的自变量很大的时候,曲线接近水平,而我们希望f(x)的取值不要太接近,以便保持较好的区分度,因此我们通常将ki设置为一个小于1的常数,也就是说函数g(z)可以表示成g(z)=1/p1·z1+1/p2·z2+……1/pn·zn,pi>1。
- 风险赋值
通常我们不会对每一个风险因素都单独赋值,而是使用一种分类的方法把风险分为高、中、低等几类。在这里,我们按照重要和紧急两个维度把风险定义为四个等级(紧急优先于重要),定义方法如下。
| 表头 | 紧急 | 不紧急 |
|---|---|---|
| 重要 | 严重 | 中 |
| 不重要 | 高 | 低 |
表-脆弱性分级
对低、中、高、严重四类风险分别赋值为1、2、3、4分。把xi记为风险赋值为i的所有赋值为i的风险赋值的综合,而对同一级别的pi可以赋值为同一常数。例如,系统有2个低危、1个中危、0个高危和3个严重风险时,则有以下结论:
x1=2·1=2
x2=1·2=2
x3=0·3=0
x4=3·5=15
- 安全分公式
最终,安全分数表达式即f(x)=100-100·EXP(-g(x))=100-100·EXP(-g(1/p1·x1+1/p2·x2+1/p3·x3+1/p4·x4)。用公式编辑器做一个漂亮的写法:
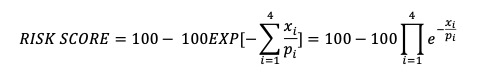
图3 算法的数学公式
2.4 使用
- 权重因子p
上一小节中我们没有讨论权重因子p,原因是在不同的系统中,p的选择会影响分数的分布(即分数更集中还是更分散),但不影响不同系统得分的排序(当然要严格遵循p1>p2>p3>p4的顺序)。为了让安全分拉开合理的差距,需要调节pi的值以让系统的表现符合主管预期的分值范围。比如你认为一个系统安全性良好应该是80分还是90分,安全性极好应该是90分还是95分,可以通过改变pi来调节。当然在不同的系统之间,pi要保持一致。
此外,qi的选择也有一些套路,当系统规模较大,qi应选择更大的数值,因为大型系统出现高风险因素的可能性更大,影响范围相比系统整体而言也有限,因此在出现相同的风险的时候,也可以考虑适当拔高安全分数(更大的qi值会算出更大的安全分数)。
当系统规模较大时,这里推荐一组pi取值,p1 = 50,p2 = 18,p3 = 12,p4 = 5。
如果感到安全分太高,可以减小pi的值,pi的值与安全分数正相关。
- Excel实现
我们可以使用Excel表格或SQL语句操作,Excel内置了指数函数表达式,使用起来非常方便。在如图所示的单元格中编辑公式:
=100-100*EXP(-(SUMIF(B2:B11,1)/D2+SUMIF(B2:B11,2)/D3+SUMIF(B2:B11,3)/D4+SUMIF(B2:B11,4)/D5))
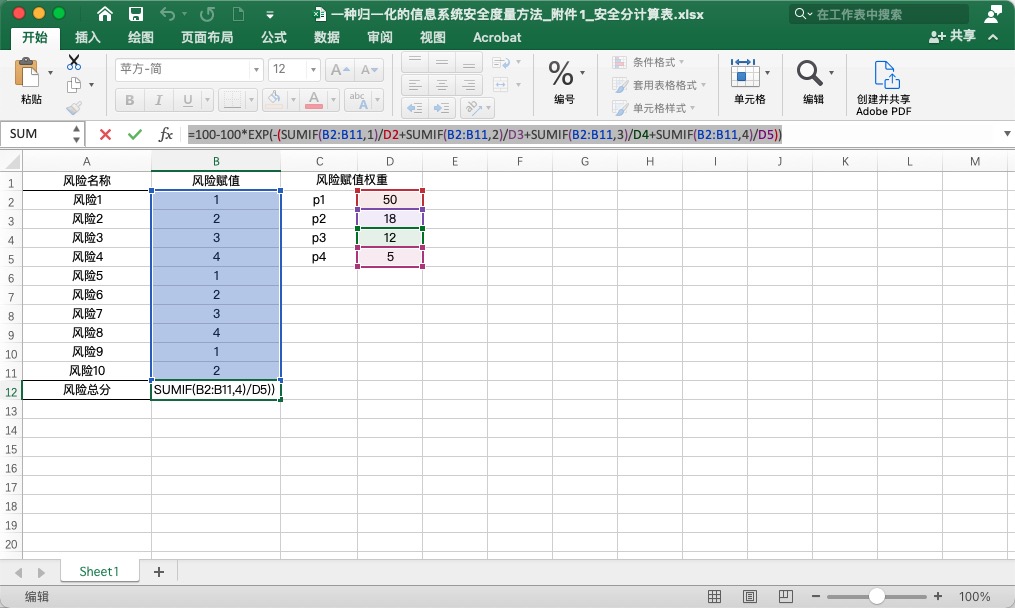
图4 Excel计算表格
- SQL实现
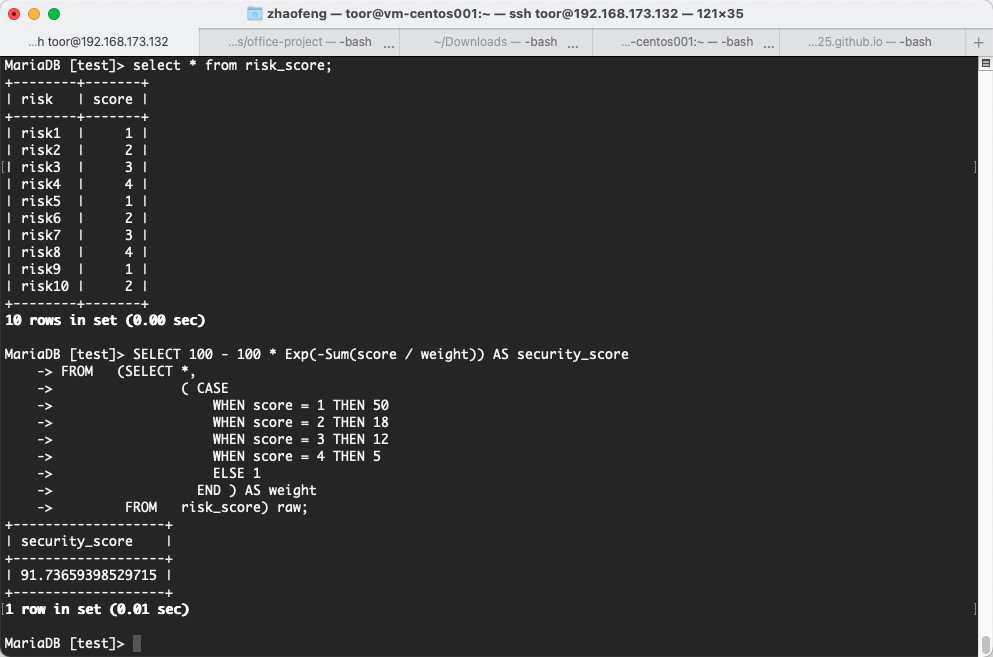
通过SQL也可以实现该算法,以上述的表格数据为例,SQL语句如下。
SELECT 100 - 100 * Exp(-Sum(score / weight)) AS security_score
FROM (SELECT *,
( CASE
WHEN score = 1 THEN 50
WHEN score = 2 THEN 18
WHEN score = 3 THEN 12
WHEN score = 4 THEN 5
ELSE 1
END ) AS weight
FROM risk_score) raw;
测试数据及运行结果如下图, 计算结果与Excel计算结果一致。
3 小结
本文介绍了一种百分制定量评价系统安全性的评分方法,该方法基于幂函数f(x)=exp(x)=e^x构建。用该方法计算的安全分,符合对高风险敏感,对风险数量呈非线性的累加效果,即风险因素越多对安全分影响越大,但单个风险因素对总分的影响减小。这样符合人们对系统安全性的一般认知,即:出现一个高风险因素时系统安全性将大打折扣,但越来越多的高风险因素叠加后对系统安全性不会继续明显扩大,同时安全分不会出现负分,只会无限接近0分。这种方法一般适用于这些场景:①多个系统的安全性的横向对比,②系统安全性变化的观测,③系统安全态势的可视化展示。目前这种方法已经在一些项目中得到应用,总体上被认可。这种方法的主要缺点在于权重系数分母pi的选取,具有一定的主观性,在大多数场合下需要不断调试取得更加理想的取值,而在多个系统上应用时,如果一旦早期的系统选定了qi的值,那么即便新的系统的计算效果不理想也不能改变,否则无法起到对比的作用。
以上是本文的全部内容,大家有问题欢迎在我的github中留言讨论(https://github.com/wangzf0225)。